Telescope Diffraction Limit: Explanation & Calculation

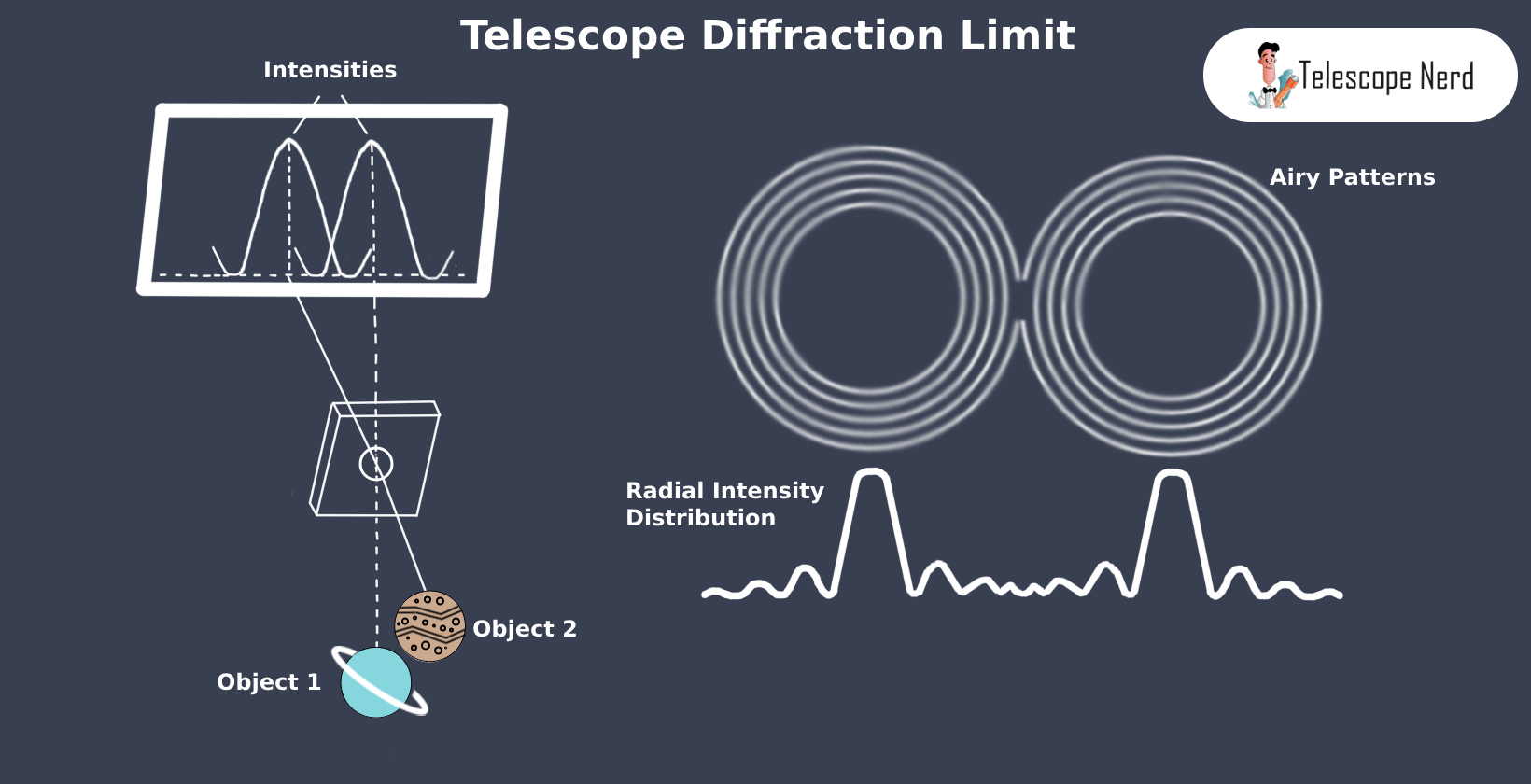
The diffraction limit is the highest angular resolution a telescope is able to achieve. This limit refers to the theoretical maximum if nothing besides the size of a telescope’s light-collecting area affects the quality of the images. This limit is a direct consequence of the nature of light waves. When light waves encounter an obstacle or aperture, such as the lens of a telescope, they bend and spread in a phenomenon known as diffraction. This bending and spreading causes a point source of light, like a star, to appear as a small disc surrounded by concentric rings of light, an effect known as an Airy pattern.

The diffraction limit is also known as the diffraction-limited resolution. It is measured in arcseconds using the wavelength of light and aperture of a telescope. The wavelength of light is typically expressed as 550 nanometers, which corresponds to green light, and the aperture is the diameter of the telescope’s primary lens or mirror. The unit of measurement for the diffraction limit is arcseconds, a unit of angular measurement. There are 360 degrees in a full circle. Each degree can be subdivided into 60 arcminutes, and each arcminute can be further subdivided into 60 arcseconds.

The diffraction limit is also influenced by the wavelength of light being observed. Shorter wavelengths (like blue light) result in smaller Airy discs and better resolution, while longer wavelengths (like red light) result in larger Airy discs and lower resolution.

The significance of the diffraction limit lies in its direct impact on the resolving power of a telescope. It sets the fundamental limit on the smallest details that are observed. For instance, two stars that are very close together in the sky will appear as a single point of light if they are closer together than the diffraction limit of the telescope. This limit is independent of the telescope’s magnification; increasing the magnification will not enable the telescope to resolve details smaller than its diffraction limit.

The diffraction limit is a key factor that determines the capabilities of a telescope. It is calculated based on the wavelength of light and the aperture of the telescope, and it directly influences the resolution of the telescope. Understanding the diffraction limit is crucial for interpreting the images captured by a telescope and for pushing the boundaries of astronomical observation.

How to Calculate Telescope Diffraction Limit?

To calculate the diffraction limit, first divide the wavelength of light by the aperture, then multiply by the Raleigh constant. The equation below provides a formula to calculate the diffraction limit of a telescope.

Diffraction Limit = 1.22 x (Wavelength of light / Aperture of Telescope)

The constant 1.22 in the formula for the diffraction limit of a telescope is often referred to as the Rayleigh criterion or the Rayleigh constant. This constant is derived from the first zero of the Bessel function, which describes the intensity distribution of the light. This distribution of light creates an intensity pattern when the light is focused, known as the Airy disk.

The Rayleigh criterion defines the minimum resolvable detail in an imaging process and is commonly used in the field of optics, including telescope design and function. In the diffraction limit equation, the wavelength of light is typically taken as 550 nanometers, which corresponds to green light. 550 nanometers is generally used because the human eye is most sensitive to green light, and it is near the middle of the visible spectrum. The aperture, on the other hand, is the diameter of the telescope’s primary lens or mirror, usually measured in millimeters.

To illustrate the calculation, consider a telescope with an aperture of 200mm. Plugging these values into the formula gives us 3.365 x 10^-6 radians. This equation is expressed as [1.22 x ((550 x 10^-9m) / 0.2 m)] = 3.365 x 10^-6 radians. To better visualize this value, astronomers convert this value into arcseconds by multiplying by a factor of 206265. This means that the telescope can resolve details as small as 0.694 arcseconds across.

The diffraction limit sets the fundamental limit on the smallest details that are resolved by a telescope. Therefore, knowing the diffraction limit helps in choosing the right telescope for specific observational needs, whether it’s observing the rings of Saturn or capturing the intricate details of a distant galaxy. It also guides the observer in setting realistic expectations about the level of detail that can be observed or photographed.

How Does Diffraction Limit Impact Telescope Resolution?

The diffraction limit directly impacts a telescope’s resolution (or resolving power) by defining the smallest detail that can be distinguished. A smaller diffraction limit means a higher resolving power, allowing the telescope to resolve finer details. Telescope resolution refers to the ability of a telescope to distinguish between two closely spaced objects in the sky. The diffraction limit directly influences this resolution.

The diffraction limit sets the minimum angular separation that a telescope can distinguish between two point light sources. For instance, if two stars in the sky are closer together than the diffraction limit of a telescope, they will appear as a single point of light. In contrast, a telescope with a smaller diffraction limit is able to differentiate between these two stars as separate points of light, even if they are very close together. This ability to distinguish between closely spaced objects is the crux of telescope resolving power.

This relationship between the diffraction limit and resolving power has practical implications in observational astronomy and astrophotography. For example, a telescope with a diffraction limit of 1 arcsecond can discern details as small as 1 arcsecond across. If two stars are less than 1 arcsecond apart, they will appear as a single point of light in this telescope. However, if the telescope has a diffraction limit of 0.5 arcseconds, it will resolve these two stars as separate points of light.

A high-resolution telescope, characterized by a small diffraction limit, will reveal intricate details such as the bands of clouds on Jupiter or the rings of Saturn. On the other hand, a telescope with a larger diffraction limit and hence lower resolution will only show these planets as featureless discs. Therefore, understanding the interplay between the diffraction limit and resolution will guide the choice of telescope for specific observational needs and set realistic expectations about the observable details.